Сегодня начинаю делать не хекслете первый проект. Результатом его, по идее, должна быть текстовая игра в терминале на решение задачек.

Первый шаг полностью посвящен подготовке к работе: нужно создать репозиторий с проектом, инициализировать нпм-пакет, установить и настроить бабель, создать исполняемый файл и опубликовать пакет в каталоге нпм.

Судя по отзывам, проекту потребуется уделить немало времени, так что на этой неделе на канале ожидается меньше постов с теорией и больше отчетов по прогрессу в работе над проектом.

Eще одно упражнение на списки, на этот раз чуть посложнее: Написать функцию, которая из вложенного списка делает плоский. Например, список типа

[1, [2, 3], 4, [5, [6, [7]]], 8] 

превращает в

[1, 2, 3, 4, 5, 6, 7, 8]

Решается передачей в reduce функции, которая по очереди цепляет элементы из первоначального списка к пустому списку. Если она встречает не примитивный элемент, а список, то рекурсивно цепляет его элементы уже к накопленному в аккумуляторе списку.

Получившийся список в конце нужно перевернуть, так как reduce комбинирует элементы начиная с первого, и последовательно цеплет последующие спереди.

В некоторых языках, кстати, предусмотрено две версии редьюса: foldl и foldr, которые начинают складывать список соответственно с левого или правого конца.

Закончил курс про последовательности. Пришло время решить парочку практических задач на списки.

Например: написать функцию, которая принимает список чисел и возвращает новый, содержащий те элементы из начального, которые имеют ту же четность, что и первое число в списке.

sameParity(l(-1, 0, 1, -3, 10, -2)); // (-1, 1, -3)
sameParity(l(2, 4, 3, -8, -5));      // (2, 4, -8)

Как получить список из элементов, удовлетворяющих определенному условию мы уже разобрали: для этого есть функция filter. Нужно лишь передать ей помимо начального списка правильную функцию, которая возвращает true для чисел той же четности, что и первое число в исходном списке.

Для этого проверяем на нечетность первое число в списке, и, в зависимости от результата, привязываем к константе isSameParity соответствующий предикат isOdd или isEven. Также не забываем вначале проверить исходный список на пустоту. Из пустого списка извлечь первое число не получится.

Map, filter, reduce — вот самые распространенные функции высшего порядка над списком. Высшего порядка они потому, что помимо списка принимают в качестве аргумента функцию. Рассмотрим, как они работают.

Map

Применяет некую функцию к каждому элементу списка.

Аргументы:

1. функция от одного аргумента,
2. список.

Результат: новый список с таким же количеством элементов, что и первоначальный.

Пример: возвести в квадрат каждое число из списка

map(square, [1, 2, 3]) // [1, 4, 9]

Filter

Отсеивает из списка элементы, которые не удовлетворяют некоторому условию. Условие выражено предикатом, который передается как аргумент в filter. Предикат — это функция, которая возвращает true или false в зависимости от переданных ей аргументов.

Аргументы:

1. функция-предикат от одного аргумента,
2. список.

Результат: новый список, содержащий некоторое количество элементов из первоначального списка.

Пример: выбросить из списка все нечетные числа

filter(isEven, [1, 2, 3]) // [2]

Reduce

Последовательно комбинирует вместе все элементы списка и некоторое исходное значение. Как именно комбинирует, задается переданной в reduce функцией. Исходное значение нужно потому что reduce пустого списка тоже должен что-то возвращать. Известен под альтернативным названием fold.

Аргументы:

1. функция от двух аргументов,
2. исходное значение,
3. список.

Результат: все что угодно. Результатом может быть какое-нибудь единичное значение типа числа или строки, может быть список с любым количеством каких угодно элементов. Никаких ограничений. Кстати, если передать в reduce определенные функции и исходные значения, то можно добиться такого же поведения как от map или filter.

Пример: сложить вместе все числа в списке

reduce(add, 0, [1, 2, 3]) // 6

Наткнулся на супер-лаконичное объяснение операций над списком при помощи эмодзи.

Прохожу на хекслете курс “последовательности”. В нем рассказывается о новом типе составных данных, который называется “список”. Cписком называется упорядоченная последовательность значений.

Составные структуры данных удобно создавать на основе пар. Вот один из способов представить с помощью пар список [1, 2, 3]:

cons(1, (cons 2, (cons 3 null)))

В такой реализации список представляет собой цепочку вложенных пар, где в каждой паре первой частью является значение из списка, а второй — следующая пара. Второй частью последней пары является значение null, которое говорит, что список кончился.

Составлять списки вручную из пар крайне муторно, поэтому используют функцию-конструктор, которая принимает элементы списка как аргументы и возвращает список, составленный из пар:

makeList(1, 2, 3)

Как и у пары, у списка есть два селектора. head возвращает первый элемент списка. tail возвращает список с отсеченным первым элементом.

Создание списка из пар возможно благодаря тому, что результат выполнения функции cons можно снова передать в качестве аргумента в другой cons. И так до бесконечности. Такое свойство называют «замыкание». Термин был заимствован из алгебры: https://ru.wikipedia.org/wiki/Замыкание_(алгебра)

Так же замыканием в программировании называют объект, хранящий функцию вместе с окружением, в котором она была создана. Эти два понятия хоть и названы одним словом, но ничего общего между собой не имеют. Сделано это чтобы все казалось немного сложнее, чем есть на самом деле.

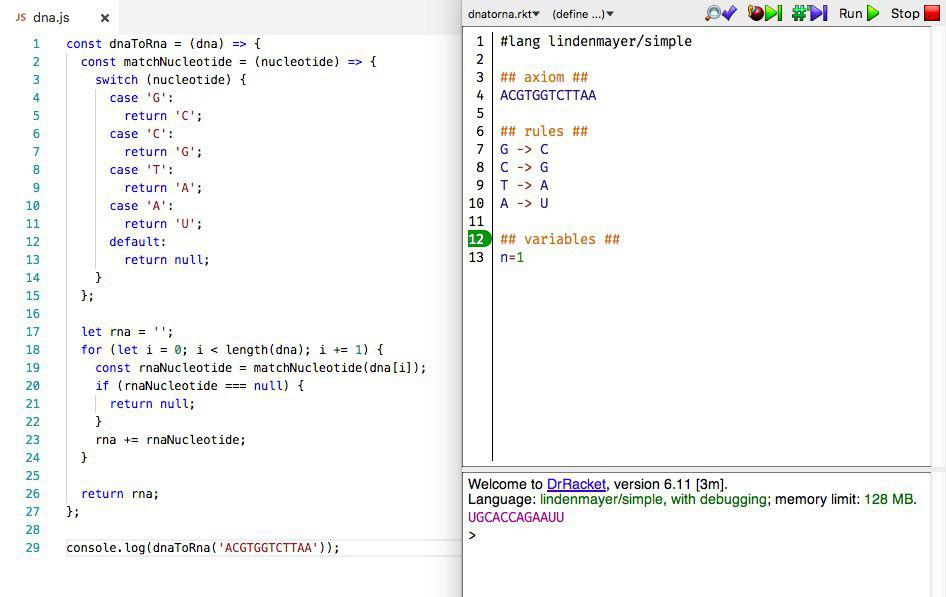
Задачи из HTDP я решаю на языке “ракет”. Это такой вариант лиспа, изначально созданный в образовательных целях, и со временем разросшийся в полноценный язык. Изучая ракет, наткнулся на прикольный язык для работы с L-системами, реализованный на нем.

Сразу вспомнил одну задачку с хекслета, в которой нужно написать функцию преобразования цепочки ДНК в РНК. Цепочка состоит из последовательности букв A, C, G, T. Преобразование заключается в замене букв:

G -> C 
C -> G
T -> A
A -> U

В итоге строка CCGTA должна превращаться в GGCAU. Как видим, ничего сложного, но задача достаточно нетривиальна чтобы задавать ее начинающим.

На скриншоте снизу мое решение на джаваскрипте и ракете. Красота использования подходящего языка в том, что решение выглядит практически как условие.

Документация языка
Про L-системы на википедии

Сегодня отвлекся немного от лямбд и поделал пару упражнений из htdp про интерактивные программы. На картинке результат одного из них: машина едет мимо деревца и телепортируется по клику мыши.

Программа разделена на две части: модель и представление. Модель — это данные, которые описывают состояние программы и функции над этим состоянием. Конкретно в этом случае состояние максимально простое — всего одно число, описывающее расстояние от левого края окна до машины. Представление — это функция, которая принимает состояние и возвращает картинку.

Нужно чтобы модель и представление были независимыми друг от друга, чтобы их можно было редактировать по отдельности.

На прошлой неделе я выкладывал сюда свое решение по реализации чисел Черча и жаловался, что не смог написать функцию вычитания единицы. Самостоятельно до решения так и не додумался, поэтому пошел искать в гугле.

Сложность тут в том, что нужно написать функцию, которая от выражения как бы убирает одно применение функции. То есть, например, из конструкции f(f(x)) получить f(x). В лямбда исчислении нет способа вместо выражения подставить пустоту, поэтому на первый взгляд задача кажется невыполнимой. Сам Черч считал, что составить такую функцию невозможно. Первым решение нашел его ученик Клини (изобретатель регулярных выражений, между прочим).

Решение заключается в том, чтобы посчитать от нуля до n, сохраняя при этом n - 1. Считать вперед мы уже умеем функцией Succ. Хранить предыдущее и текущее значение можно при помощи пар.

Берем пару (Zero, Zero), назовем ее p для краткости. Заменяем ее на (second(p), Succ(second(p)). Повторяем процедуру n раз. На выходе получается пара (n - 1, n). А n - 1 — это как раз то значение, которое нам и нужно, вытаскиваем его селектором first.

Имея функцию для вычитания единицы несложно написать функцию вычитания одного числа из другого. Посмотреть на эти функции вживую: https://repl.it/@buyfn/Church-arithmetic.

Пока изучал вопрос, нашел статью, где автор утверждает, что нашел несколько других, более простых, способов выразить эту же функцию. Я, признаться, не смог их понять. Возможно, сможете вы: http://okmij.org/ftp/Computation/lambda-calc.html.

Закончил курс о составных данных. Самое крутое там идет в конце — реализация пар на джаваскрипте. Вот один из способов: https://repl.it/@buyfn/Pairs

Что самое удивительное, в определениях функций нет ни одной константы или переменной. Тем не менее это не мешает их использовать для хранения данных. Фишка в том, что при вызове cons создается новая функция, которая помнит, что было передано в cons, который ее создал.